기술의 반대말은 무엇 일까요? 철학 일까요? 예술 일까요? 정확한 반대말이 없다는 정답을 알고 있는 사람이라도 왠지 예술을 떠올릴 수 있을 것 같습니다.
그럼에도 불구하고 기술은 다른 분야에서와 비슷하게 예술쪽에도 지대한 영향을 미치고 있습니다.

예전에야 전통적인 접근 만이 예술성을 지킬 수 있을 것으로 비추어지던 시대도 있었고, 현재도 일부 보수적인 시각에서 예술을 그저 사람의 감성에 호소해야 한다는 태도도 있습니다만, 결국 표현의 방식, 표현을 인식하는 형태에 대한 기술적인 접근이 이루어지면서, 기술의 영향력은 아마도 더 커질것으로 예상됩니다.
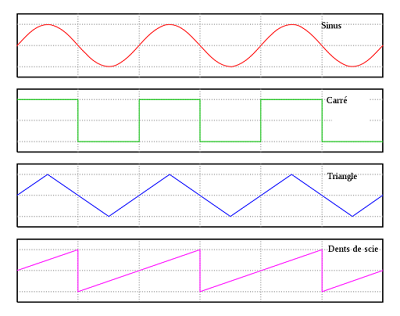
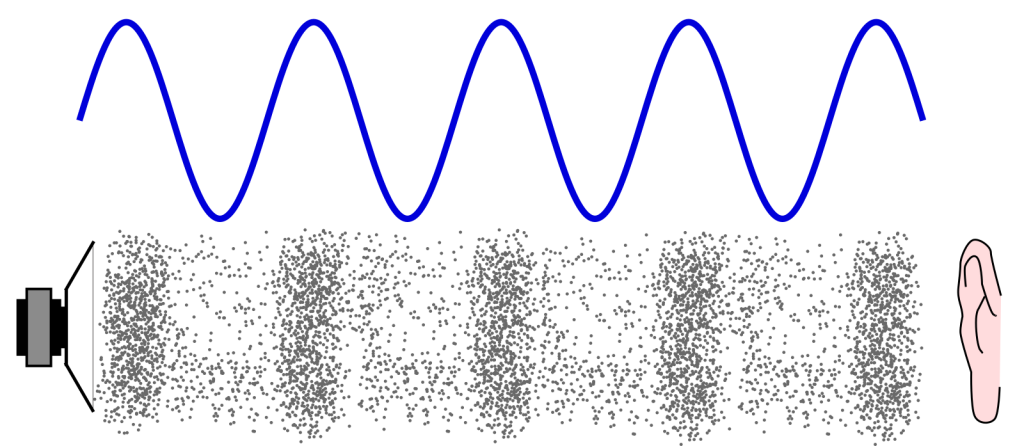
예술에 대한 도전적인 기술 적용은 특히나 음악에서 두드러져 보입니다. 사실 기술적인 도전이 이루어질 수 있는 배경에는 표현 방식에 대한 기술적인 분석과 이론적인 정립이 선행 되어야 하는데, 바로 음악이 오랫동안 그런 노력을 해오고 있던 분야이기 때문일 것 입니다.
특히나 음악이라는 예술적 장르는 음향 으로 부터 시작해서 화성학등 까지 많은 이론들이 잘 정립되어 있어 보입니다. 이러한 이론들이 있으므로 해서 그 내용이 교과과정에 편성되어 어린이 부터 청소년 까지 체계적으로 접근할 수 있으며, 교과과정 이후 성인이 되어서도 각광받는 취미가 되기에 손색없는 자료들을 가지고 있는 것은 음악이 기술과 융합 되기에 손색이 없는 것은 당연해 보이기도 합니다.
하지만 여전히 음악은 예술적 영역 만을 고집하는 여러 부류가 존재할 뿐만 아니라, 이때까지 만들어진 이론에 대한 지속적인 연구와 도전이 이루어지지 않는 문제점도 존재하고 있습니다. 특히나 음악 이론에 관련해서는 워낙 오랜동안 연구 되어 왔던 분야 였던 탓에 더 이상 기존의 이론에 대한 새로운 해석이나 도전이 이루어지지 않고 있습니다.
이 블로그에서는 성인이 된 이후 가장 인기 있는 악기로 인식되는 기타를 기초로 음악적인 부분과 음악 이론을 보다 이해하기 쉽게 정리하고, 기술적인 접근방식을 통하여 새로운 시각으로 음악을 생각할 수 있도록 하는데 보탬이 될 수 있는 자료를 제공하고자 합니다.
음계 “도 레 미”를 모르고 그게 안들린다면 과연 우리는 음악을 듣는다고 이야기 할 수 있을까? 라는 질문에 어떻게 답할 수 있을까요?